Aufgaben

Willkommen bei der Aufgabendatenbank! Sie sind unsicher in der Physik und brauchen dringend mehr "Stoff" zum üben? Dann sind Sie hier richtig.




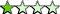
Aufgabe 421 leicht

Figur

Wie gross ist die Geschwindigkeit des Fahrzeugs mit dem folgenden Ort-Zeit Diagramm

  1. in `(km)/(h)`? (`10(km)/(h)`)
  2. in `m/min`? (`166 2/3m/min`)
  1. Das Fahrzeug kommt in 60 Minuten (15-5)km weit. Also in einer Stunde 10 km. Die Geschwindigkeit beträgt also `10(km)/(h)`.
  2. `10(km)/(h)` entsprechen `(10\'000m)/(60min)=166.bar7m/min`.
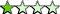
Aufgabe 422 leicht

Erstellen Sie jeweils das Ort-Zeit Diagramm für die gleichförmigen Bewegungen mit folgenden Geschwindigkeiten, wobei die Bewegung von den Achsenschnittpunkten ausgehen sollen.

  1. `2m/s` (k.A.)
  2. `5m/s` (k.A.)
  3. `36(km)/(h)` (k.A.)
  4. `0.9km/min` (k.A.)
  1. Siehe Diagramm.

    Figur

  2. Siehe Diagramm.
  3. `36(km)/(h)hat=10m/s`, Rest siehe Diagramm.
  4. `0.9km/min=15m/s`, Rest siehe Diagramm.
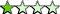
Aufgabe 423 leicht

Figur

Betrachten Sie das folgende Ort-Zeit Diagramm:

  1. Wie lautet das Ort-Zeit Gesetz der Bewegung? (k.A.)
  2. Erstellen Sie das Geschwindigkeits-Zeit Diagramm! (k.A.)
  3. Wo befindet sich das Objekt nach zwei Stunden? (`24.02*10^3m`)
  1. Wir wählen zwei beliebige Punkte auf der Geraden aus, um deren Steigung - also die Geschwindigkeit des bewegten Objekts - zu ermitteln: `t_1=0s`, `s_1=20m` und `t_2=6s`, `s_2=40m`. Die Geschwindigkeit ermittelt sich damit zu `v=(Deltas)/(Deltat)=(40m-20m)/(6s-0s)=(20m)/(6s)=3 1/3m/s`. Die Weltlinie geht nicht durch den Koordinatenursprung, sondern besitzt einen Achsenabschnitt auf der Ortsachse von `s_0=20m`. Mit diesen Angaben ergibt sich für das Ort-Zeit Gesetz `s=20m+3 1/3m/s*t`
  2. Die Geschwindigkeit beträgt konstant `v=3 1/3m/s`.

    Figur

  3. Nach zwei Stunden, also nach `2h*3600s/h=7200s` befindet sich das Objekt am Ort `s=20m+3 1/3m/s*7200s=24020m`.
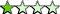
Aufgabe 424 leicht

Figur

Betrachten Sie das folgende Ort-Zeit Diagramm:

  1. Ordnen Sie die Punkte im folgenden Ort-Zeit Diagramm nach steigenden Geschwindigkeitsbeträgen, welche das bewegte Objekt zum bezeichneten Zeitpunkt hatte. (k.A.)
  1. Die Steigung in den einzelnen Punkten betrachten: $$c=d=e < b < a$$
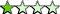
Aufgabe 470 leicht

Figur

In einem Ort - Zeit Diagramm sind die Bewegungen von 2 Körpern a) und b) aufgezeichnet.

  1. Welche Geschwindigkeit besitzt Objekt a)? (`5m/s`)
  2. Wann und wo kreuzen sich die beiden Objekte? ((100m,20s) und (300m,60s))
  3. Wann haben die beiden Körper dieselbe Momentangeschwindigkeit? (Abschätzen, aber begründen!) (`~~40s`)
  4. In welchem Zeitintervall ist die mittlere Geschwindigkeit von Körper b) gleich der Geschwindigkeit von Körper a)? (20s - 60s)
  1. Das Objekt legt eine Strecke von 300m in 60s zurück. Die Geschwindigkeit beträgt also `v=(Deltas)/(Deltat)=(300m)/(60s)=5m/s`.
  2. Die beiden Objekte kreuzen sich an zwei Orten: einmal am Ort 100m nach 20s und ein weiteres Mal am Ort 300m nach 60s.
  3. Die Steigung der Kurve im Ort - Zeit Diagramm entspricht der Geschwindigkeit. Die Steigung der Kurve ist etwa zum Zeitpunkt `t=40s` gleich der Steigung der Geraden.
  4. Zwischen den beiden \"Treffpunkten\": beide Objekte bewegen sich in der Zeit von 20s bis 60s vom Ort 100m zum Ort 300m.
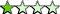
Aufgabe 472 leicht

Figur

Nebenstehende Abbildung zeigt ein Geschwindigkeit - Zeit Diagramm.

  1. Welche oder welches der darunter abgebildeten Ort - Zeit Diagramme passen dazu? (n.A.)
  1. Die Geschwindigkeit beträgt innherhalb der ersten 2s `2m/s`. Das Objekt legt also innerhalb dieser Zeitspannen eine Strecke von 4m zurück und bleibt dann für 3s am selben Ort. Damit scheiden bereits die Möglichkeiten b) und c) aus. Von 5s bis 7s fährt das Objekt mit einer Geschwindigkeit von `-3m/s`, legt also den Weg -6m zurück, bevor es wieder verweilt. Damit kommen die Lösungen a) und d) in Frage, bei beiden Diagrammen sind diese Voraussetzungen erfüllt.
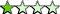
Aufgabe 475 leicht

Figur

Betrachten Sie nebenstehendes Ort - Zeit Diagramm.

  1. Wie lautet das Ort - Zeit Gesetz? (k.A.)
  2. Zeichnen Sie das Geschwindigkeit - Zeit Diagramm. Verwenden Sie für jeweils eine Einheit 1cm auf beiden Achsen! (k.A.)
  3. Wie weit vom Ursprung weg befindet sich das Objekt nach 1 Stunde und 15 Minuten? (`30010m`)
  1. Die Geschwindigkeit ermittelt man zu `v=(40m)/(6s)=6 2/3m/s`. Der Achsenabschnitt auf der s - Achse beträgt 10m. Das Ort - Zeit Gesetz lautet also `s = 10m+6 2/3m/s*t`.
  2. Die Lösung sieht wie folgt aus:

    Figur

  3. Eine Stunde und 15 Minuten sind 75 Minuten oder `Deltat=75min*60s/min=4500s`. Eingesetzt in das Ort-Zeit Diagramm aus a) bekommt man `s = 10m+6 2/3m/s*4500s=30010m`
Aufgabe 488 leicht

Das Ohr kann Schallempfindungen deutlich trennen, wenn ihr zeitlicher Abstand nicht unter einer Zentelsekunde liegt.

  1. Wie weit muss eine den Schall reflektierende Felswand mindestens entfernt sein, damit man ein deutliches Echo wahrnehmen kann? (17m)
  1. Die gesamte Strecke des Schalls zur Felswand und zurück sei s, dann gilt `s=c_(Schall)*1/2Deltat=17m`, mit `c_(Schall)=340m/s` .
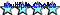
Aufgabe 498 leicht

Figur

Das Diagramm verdeutlicht die linearen Bewegungen eines Körpers. Welche der folgenden Aussagen sind richtig?

  1. Der Körper bewegt sich mit gleichbleibender Geschwindigkeit.
  2. Der Körper bewegt sich mit zunehmender Geschwindigkeit.
  3. Der Körper hat die Geschwindigkeit 10 m/s.
  4. Der Körper hat die Geschwindigkeit 5 m/s
  5. Der Körper hat die Geschwindigkeit 2.5 m/s
  1. 1
  2. keine Angaben
  3. keine Angaben
  4. keine Angaben
  5. keine Angaben
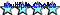
Aufgabe 499 leicht

Figur

Das Diagramm verdeutlicht die Bewegungen zweier Körper A und B. Welche der folgenden Aussagen sind richtig?

  1. Körper A überholt Körper B.
  2. Körper A und B fahren in entgegengesetzte Richtung.
  3. A fährt mit 2,5 `m/s`.
  4. A fährt mit `5 m/s`.
  5. A und B sind gleichzeitig losgefahren, aber B hatte Vorsprung.
  6. A und B sind vom gleichen Ort losgefahren, A aber später.
  1. Die Weltlinie von A ist steiler als die von B: A ist schneller unterwegs. Am Schnittpunkt der beiden Geraden wird B von A überholt. Die Antwort ist also richtig!
  2. Falsch - die Steigungen der Weltlinien sind in beiden Fällen positiv, was gleichbedeutend mit einer positiven Geschwindigkeit ist.
  3. Falsch, s. nächste Antwort.
  4. Richtig: A legt in 10 Sekunden 50 m zurück.
  5. Falsch, beide Weltlinien beginnen am Ort `x=0` - kein Vorsprung.
  6. Richtig, die Weltlinie von B schneidet die Zeitachse bei `t=0`, diejenige von A bei `t>0` - A ist später losgefahren.
< <Zurück (1) (2) Vorwärts > >

Copyright © physica.ch

Datenschutzerklärung